探索图形 五（3） 韦昕言

        最近一张卷子上的题目引起了我的注意。

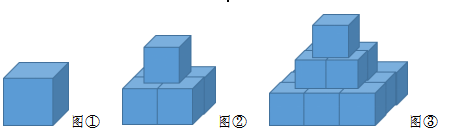
        题中第一幅图是一个棱长为1厘米的小正方体，第二幅图底下多了第二层2×2的4个小正方体，第三幅图又多出第三层3×3的9个小正方体。以此类推，问第10幅图有几个小正方体，第20副图的表面积是多少？

        乍一看，第一问较为简单，而第二问计算起来更加繁琐。其实不然。前者是1²+2²+3²+…+10²，计算起来较为麻烦。而后者思路容易理清，计算起来也不麻烦：第20幅图一共有20层，前、后、左、右四个面完全相同，都是一个面两个面三个面一直加到二十个面，用等差数列求和公式列式（1×1）×（1+20）×20÷2得出结果210cm²是一个面的面积，再乘4，840cm²就是前、后、左、右四个面的面积。下面则是那20×20的大正方形。那上面呢？不妨想象一下，如果俯瞰这个立体图形会是怎么样子。那应该是是一个大正方形。而它的边长呢？正是20cm。于是第20幅图的表面积应该是840+20×20×2=1640（cm²）。

         至于第一道题，硬算得出

        1²+2²+3²+…+10²为1+4+9+16+25+36+49+64+81+100=385（个）。

       这个式子是有巧算方法的：

        1+4+9+16+25+36+49+64+81+100

=（1+4+9+16）+25+（36+64）+（49+81）+100

=30+25+100+130+100

=360+25

=385（个）

        这只是比较简单的凑数法。其实像这种多个平方数相加的式子还有个公式：

        1²+2²+3²+…+n²=n(n+1)(2n+1)/6 

         正所谓“人不可貌相，海不可斗量。”有些题看似简单，实际上却很难；有些题看似很难，实际上却很简单。事物的表面是具有欺骗性的，我以前就常常被坑过：那些看似简单却很难的题随随便便就答题了，却被那些看似很难却很简单的题吓倒。看来，我得重视这个问题啊！