几何学的基石--勾股定理 五三班 肖韶仪

         中国是发现和研究勾股定理的最古老的国家之一，中国古代著名数学家商高也曾经提出过非常容易记忆及利用起来的名句：“若勾三股四，则弦五”。所以勾股定理在中国又叫做“商高定理”。勾股定理从古代起就有着非常广泛的应用，根据历史记载，大禹在治水的过程中，利用勾股定理来计算两处水位的高低差，从而决定水流走向，最后使洪水注入海中，不再有大水泛滥的灾害。除了中国外，古巴比伦人、古埃及人、古希腊人也都曾独立发现过勾股定理。欧几里得著作的《几何原本》中给出了勾股定理的证明，这也是目前有记录在书上的最早证明之一了。

       勾股数指的是一组正整数，他们能够构成直接三角形的三条边的边长。常见的勾股数有（3，4，5—勾三股四弦五），（5，12，13），（7，24，25），（9，40，41），等等。这些勾股数都满足a²+b²=c²的规律，而这个规律又称之为勾股定理了。

      勾股定理的证明方法有非常多种，古往今来，从平民百姓到帝王将相，喜欢数学或者几何的人都愿意探讨和研究它的证明。其中较为有名的有毕达哥拉斯的证明以及赵爽弦图。

       毕达哥拉斯的证明如下：

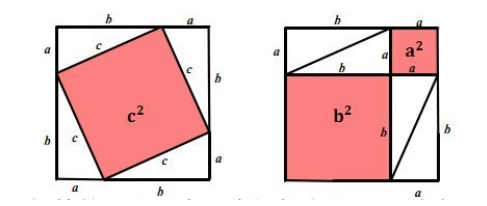
      由上图可见，左图可以得到大正方形的面积为2ab+c²，右图得到大正方形的面积为a²+ b²+2ab，所以可以证明a²+ b²= c²。

     赵爽弦图如下：

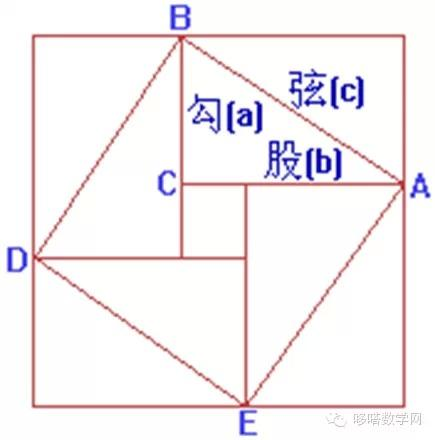
     大正方形的面积为c²，同时又是4个小三角形面积(单个面积为ab/2)加上中间的小正方形的面积（a-b）²之和，即c²=2ab+（a-b）²= a²+ b²。

    相比之下，赵爽弦图的证明方式更为简明和直观，也体现了中国古代的数学发展的水平。