探索图形 五8班 杜玥熹

    引子：最近我看到了一道有关探索图形的题目，对它做了以下的分析。

     题目与现象：用棱长1cm的小正方体拼成如下的大正方体后，把它们的表面分别涂上颜色，1、2、3中，三面、两面、一面涂色以及没有涂色的小正方体各有多少块？将结果填入下表中。

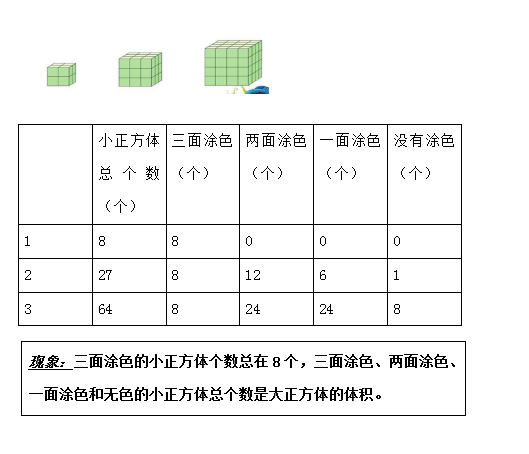
      分析：如果一个大的正方体每条棱上有n个（n大于等于 3）个小正方体，则：1.三面涂色的小正方体，每个顶点上有一块，共8块。｛共8个顶点｝2.两面涂色的小正方体，每条棱上有（n-2）块，共12（n-2）块。｛共12条棱｝3.一面涂色的小正方体，每个面中有（n-2）的平方块，共有6（n-2）块｛共6个面｝。4.无色的小正方体位于大正方体内部，完全无接触的地方，共（n-2）的3次方块。

      结论：若设大正方体的棱长为ncm，则它小正方体的个数（即是大正方体的体积）为n的三次方，三面涂色的其实在大正方体的顶点上，（它露出来上面或下面、正面和侧面三个面）正方体共有8个顶点，故三面涂色的小正方体个数为8个。两面涂色在棱上，故有12（n-2）块。一面涂色的在面中，6（n-2）的平方块，无色的位于大正方体内部，（n-2）的3次方块。