有趣的平行线 五（7）班  林靖媛 翁新玥 何至平 吕菲儿

有趣的平行线

五（7）班  林靖媛 翁新玥 何至平 吕菲儿

        上学期，我在数学书上看到了佐尔拉错觉的图片，于是我开始对佐尔拉错觉产生了兴趣并想了解它。

        佐尔拉错觉是指一些平行线由于一些附加线段的影响而看成不平行的现象。对于这类几何错觉，神经生理学理论认为，当两个轮廓彼此接近时，它们在视网膜上的投影也彼此接近，造成视网膜上的神经细胞间存在互相抑制的现象出现，进而引起几何图形形状和方向的错觉。  如下图：

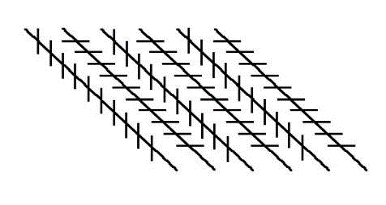
        佐尔拉错觉是由欧几里德发现的平行线的基础上经过后人的探究发现的一种错觉。研究发现，当佐尔拉图形中平行与干扰线的夹角从0度到90度之间都能观察到佐尔拉错觉，但在夹角为20度到60度时，佐尔拉错觉最明显，当夹角为45度时，产生的佐尔拉错觉最强烈。

         通过对佐尔拉错觉的了解，我对平行线也引起了兴趣。到底什么是平行线呢？

         几何中，在同一平面内，永不相交（也永不重合）的两条直线(line)叫做平行线（parallel lines）。如果两条直线都与第三条直线平行，那么这两条直线也互相平行。如若a∥b，b∥c，则a∥c。

         平行线公理是几何中的重要概念。欧氏几何的平行公理，可以等价的陈述为“过直线外一点有唯一的一条直线和已知直线平行”。而其否定形式“过直线外一点没有和已知直线平行的直线”或“过直线外一点至少有两条直线和已知直线平行”，则可以作为欧氏几何平行公理的替代，而演绎出独立于欧氏几何的非欧几何。

         欧几里德是古希腊著名的数学家, 他在其名著《几何原本》一书中, 列出了五个公理在欧几里德的几何原本中，第五公设（又称为平行公理）是关于平行线的性质。它的陈述是：两直线 AB、CD 被另一直线截于 E、F, 若∠ AEF+∠ CFE< 180° , 则两直线在 EA、FC 的方向相交。

         这条公理的陈述过于冗长。在1795年，苏格兰数学家Playfair提出了以下公理作为平行公理的代替，在被人们广泛的使用。“在同一平面内，过直线外一点，而且只有一条直线与这条直线互相平行。”

        平行公理的推论： “ 如果两条直线都和第三条直线平行，那么这两条直线也互相平行。可以简称为：平行于同一条直线的两条直线互相平行。”

        平行线在生活中到处都是，比如，铁轨，跑道，双杠，等等。如果跑道不是平行的而是相交的，那么运动员将会撞在一起。正是平行线，我们的生活才变得井井有条，多姿多彩。数学其实在我们的生活中无处不在，你们还能在生活中找到和平行线有关的东西吗？